Poisson 2D Triangulation in Linear Time and Memory

Introduction

Some computer graphics applications require random, yet somehow regular meshes – examples include material simulation or surface reconstruction.

Poisson disc sampling is excellent for creating a vertex field with tight upper and lower limits on the distance between neighboring vertices (a.k.a. 2D blue noise). Such a sampling also guarantees that, on average, every vertex has six neighbors.

But how to connect these vertices? Requirements normally include:

• no isolated vertices – at least three connections per vertex, and six on average
• no disconnected islands
• no crossings/overlaps

This is usually solved with Delauney triangulation. In general, 2D Delauney triangulation has a runtime of O(n log n), but you can get down to O(n log log n) in special cases like uniform random distribution. My problem with Delauney, however, is its high complexity.

If you use a grid to accelerate the generation of the 2D Poisson distribution, you can recycle this grid to speed up the triangulation. It won’t be perfect, but the algorithm is cache-friendly and extremely fast. It runs in O(n) time and memory.

It runs a scan line through the grid and adds triangles to the graph as it encounters new vertices. Both the total number of triangles and the maximal number of vertices in the scan line are limited by properties of the distribution, so no dynamic memory allocation needs to take place in the inner loop.

Prerequisites

X points right and Y points up. Triangles are defined in clockwise order.

The Poisson distribution must be created using a 2D grid as explained in Fast Poisson Disk Sampling in Arbitrary Dimensions. You want to do this anyway because it generates points in O(n) time and memory.

The distance between neighbors must be in [r, 2r] range, as is normal for Poisson.

Limitations

Unlike Delauney triangulation, this algorithm will not always generate optimal triangulation. In my tests, 2 % of triangle edges turned out longer than 2r. 20 % of triangles could be improved by flipping edges with their neighbor.

Don’t use this algorithm if this is a problem for you!

There should be samples at the outer bounds of the field or the edges will turn out horribly deformed. Note that this same limitation applies to constrained Delauney. The images in this article place samples in regular intervals at the outer edges.

There must be at least two lines and two columns in the grid.

Initialization

Start at y_grid = 0. Traverse the grid towards positive X for vertices and connect them to a Wavefront. A wavefront is a polyline along samples that forms the orange line moving upwards in the animation above. Its size is limited to width_grid vertices (TODO: Proof!), so reserve this upfront.

Note that the total number of triangles in the graph is limited to six times the number of samples. Reserve this, too, and there will be no memory allocation in the inner loop.

Inner Loop

Iterate all grid lines towards positive Y. Iterate each grid line towards positive X. If you encounter a vertex, find the vertex in the wavefront just below and left to it by iterating the wavefront until v_it.x < v_new.x.

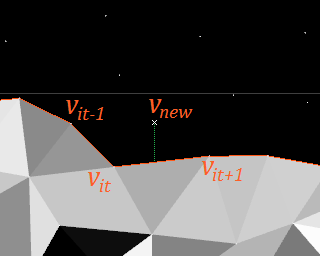
Now either add a new vertex to the wavefront or replace an existing one. In doing so, it will create either one or two triangles.

Replace Wavefront Vertex

In the best case, v_it can be replaced with v_new, creating two new triangles. This is the best case because it does not change the length of the wavefront and allows to optimize the proportions of the new triangles.

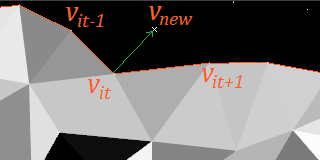
You should, in particular, check both distances d(v_it+1, v_it-1) and d(v_new, v_it) and generate the triangles along the shorter edge!

Note that the wavefront must satisfy several requirements for this to be legal:

• v_it must not be the first vertex in the wavefront.
• v_it must be lower than its left neighbor v_it-1. I.e., the edge must be concave.
• Both distances d(v_it-1, v_new) and d(v_new, v_it+1) must be smaller than 2r (or the operation would generate triangles that are too stretched).

Create Wavefront Vertex

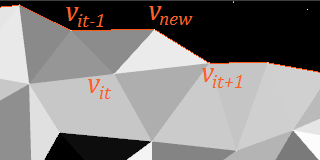
If the above is not possible, try extending the wavefront by a new vertex:

Wavefront Cleanup

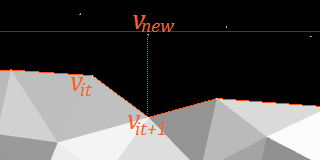
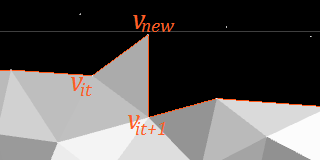
After traversing a grid line, the wavefront may have more vertices than before. This is a dangerous trend that, if continued, would totally fragement the wavefront.

If there is a cavity – a vertex that is farther than 1.28 r below the current line – then there was no good triangulation for it. Flatten the cavity by creating a new triangle above it, connecting its left and right neighbors in the wavefront.

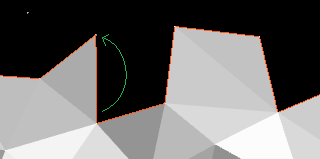
I found that triangulation quality improves if you also remove any concave vertices, given the lengths of the new triangle edges are all below 2r. You can determine if two edges are concave by computing the signed area of the parallelogram they span – it is negative for concave edges.

The factor of 1.28 was determined experimentally. 1.0 makes one percent of triangles worse.

Wavefront cleanup could be combined with wavefront operations above (specifically, cleanup could run while the wavefront is traversed to find the segment just below a new sample), but I didn’t bother doing it yet.

Pseudocode

// Initialization
create_poisson_2d(points, w, h, grid, wgrid, hgrid)

// Initialize the wavefront with the first grid line:
list_of_indices wavefront;
for vertex_index in grid.lines[0]
	wavefront.add(vertex_index)

for line in grid.lines(1...hgrid)
	// If this line starts with a new point, move the wavefront there. This saves us from handling special cases later on.
	if is_set(line[0])
		add_triangle(wavefront[0], line[0], wavefront[1])
		wavefront[0] = line[0]
	// Process all vertices in this line:
	wavefront_it = &wavefront[0]
	for x in 1...wgrid
		if not is_set line[x]
			continue;

	// Found a vertex. Find the beginning of the corresponding line segment in the wavefront.
	new_vertex_index = line[x]
	while points[wavefront_it[1].x < points[new_vertex_index].x
		++wavefront_it;

	// Decide whether to move an existing vertex or to create a new one.
	if wavefront_it >= &wavefront[1] && points[wavefront_it[-1]].y > points[wavefront_it[0]].y // left vertex is lower than its left neighbor
	&& dist(points[wavefront_it[-1]], newVertex) < 2 * r && dist(points[wavefront_it[1]], newVertex) < 2 * r

		if dist(points[wavefront_it[0]], newVertex) < dist(points[wavefront_it[-1]], points[wavefront_it[1]])
			add_triangle(wavefront_it[-1], new_vertex_index, wavefront_it[0])
			add_triangle(wavefront_it[0], new_vertex_index, wavefront_it[1])
		else
			add_triangle(wavefront_it[-1], new_vertex_index, wavefront_it[1])
			add_triangle(wavefront_it[-1], wavefront_it[1], wavefront_it[0])
		wavefront_it[0] = new_vertex_index;

	else // create new vertex
		add_triangle(wavefront_it[0], new_vertex_index, wavefront_it[1])
		wavefront.remove(wavefront_it + 1)
		wavefront_it[1] = new_vertex_index

	// If this line ends with a new point, move the wavefront there. This saves us from handling special cases above.
	if is_set line[wgrid - 1]
		add_triangle(line[wgrid - 1], wavefront[wavefront.length - 1], wavefront[wavefront.length - 2])
		wavefront[wavefront.length - 1] = line[wgrid - 1]

	// Fill any cavities in the wavefront.
	wavefront_it = &wavefront[0]
	final_y = y / hgrid * h - 1.28f * r // any point below this coordinate was not triangulated correctly
	for wavefront_it in &wavefront[0]...&wavefront[wavefront.length - 2]
		is_stretched = dist(points[wavefront_it[0]], points[wavefront_it[2]]) > 2 * r
		is_concave = signedArea(points[wavefront_it[0]], points[wavefront_it[1]], points[wavefront_it[2]]) < 0
		if points[wavefront_it[1]].y < finalY
			add_triangle(points[wavefront_it[0]], points[wavefront_it[2]], points[wavefront_it[1]])
			wavefront.remove(wavefront_it + 1)